Polya urn model
In statistics, a Polya urn model (also known as a Polya urn scheme or simply as Pólya's urn), named after George Pólya, is a type of statistical model used as an idealized mental exercise to understand the nature of certain statistical distributions.
In an urn model, objects of real interest (such as atoms, people, cars, etc.) are represented as colored balls in an urn or other container. In the basic urn model, the urn contains x white and y black balls; one ball is drawn randomly from the urn and its color observed; it is then placed back in the urn, and the selection process is repeated. Questions can then be asked about the probability of drawing one color or another, or some other properties.
The Polya urn model differs only in that, when a ball of a particular color is drawn, that ball is put back along with a new ball of the same color. Thus, unlike in the basic model, the contents of the urn change over time, with a self-reinforcing property sometimes expressed as the rich get richer.
Note that in some sense, the Polya urn model is the "opposite" of the model of sampling without replacement. When sampling without replacement, every time a particular value is observed, it is less likely to be observed again, whereas in a Polya urn model, an observed value is more likely to be observed again. In both of these models, the act of measurement has an effect on the outcome of future measurements. (For comparison, when sampling with replacement, observation of a particular value has no effect on how likely it is to observe that value again.) Note also that in a Polya urn model, successive acts of measurement over time have less and less effect on future measurements, whereas in sampling without replacement, the opposite is true: After a certain number of measurements of a particular value, that value will never be seen again.
- beta-binomial distribution: The distribution of the number of successful draws (trials), e.g. number of extractions of white ball, given
draws from a Polya urn. - multivariate Pólya distribution (also known as the Dirichlet compound multinomial distribution): The distribution over the number of balls of each color, given draws from a Polya urn where there are
different colors instead of only two. - martingales, the Beta-binomial distribution and the beta distribution: Let w and b be the number of white and black balls initially in the urn, and
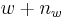the number of white balls currently in the urn after n draws. Then the sequence of values 
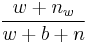for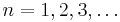 
is a normalized version of the Beta-binomial distribution. It is a martingale and converges to the beta distribution when n → ∞. - Dirichlet process, Chinese restaurant process: Imagine a modified Polya urn scheme as follows. We start with an urn with
black balls. When drawing a ball from the urn, if we draw a black ball, put the ball back along with a new ball of a new non-black color randomly generated from a uniform distribution, and consider the newly generated color to be the "value" of the draw. Otherwise, put the ball back along with another ball of the same color, as for the standard Polya urn scheme. The colors of an infinite sequence of draws from this modified Polya urn scheme follow a Chinese restaurant process. If, instead of generating a new color, we draw a random value from a given base distribution and use that value to label the ball, the labels of an infinite sequence of draws follow a Dirichlet process.